Définition
. Ce nombre irrationnel (donc qui ne peut pas s’écrire sous la forme d’une fraction de deux entiers) est l'unique solution positive de l'équation
x2 - x – 1 = 0.
Il vaut exactement :
(1 +ⱱ5) / 2, soit approximativement : 1,618 033 988 749 894 848 204 596 63 ou plus simplement 1,618 034.
On le note : φ (phi), la lettre grecque ayant été choisie en l’honneur de Phidias, l'architecte grec du Parthénon.
. Le nombre d'or est la valeur de proportion qui pourrait être qualifiée de "naturelle", définie en géométrie comme l'unique rapport a / b entre deux longueurs a et b telles que le rapport de la somme a + b des deux longueurs sur la plus grande (a) soit égal à celui de la plus grande (a) sur la plus petite (b) c'est-à-dire :

Il possède plusieurs particularités arithmétiques intéressantes :
1 / φ = φ – 1 1 / 1,618034 = 0.618034
φ * φ = φ + 1 1,618034 * 1,618034 = 2,618034
φ / (φ - 1) = φ + 1 1,618034 / 0,618034 = 2,618034 = 1,618034 + 1
φ3 = φ2 + φ = 2φ + 1
φ4 = φ3 + φ2 = (2φ+1)+(φ+1) = 3φ + 2
φ5 = 5φ + 3
φ6 = 8φ + 5
φ7 = 13φ + 8
(φ + 1) * 12 / 10 = ~ Π 2,618034 x 12 / 10 = 3,14164… = ~ Π
12 / 10 = Intervalle musical de tierce (entre gamme majeure et gamme mineure)

On trouve plus de publications consacrées à φ que dédiées à π, mais c'est sans doute parce que φ est plus élémentaire et qu'il est associé à certaines croyances numérologiques.
La saga du nombre d’or
. Les grands mathématiciens en ont parlé sagement. Son histoire est une véritable saga qui court sur plusieurs millénaires. Les premières traces écrites du nombre d’or se trouvent dans les célèbres « Éléments » d’Euclide, au 3e siècle av.JC, qui proposent un état structuré des mathématiques de l’époque. C’est le critique d’art britannique Théodore Cook qui, en 1914, le baptisa) Phi (φ) en l’honneur de Phydias, l’architecte du Parthénon.
. Trois siècles auparavant, les pythagoriciens, à l’aube du siècle de Périclès, avaient fondé une école de pensée basée sur les nombres et leurs rapports qui a largement influencé la mentalité grecque. En attribuant un nombre à chaque chose, les pythagoriciens font du nombre le concept central de la nature et auraient donc cherché (on ne dispose pas d’écrits, car ils avaient le goût du secret), à expliquer le cosmos par des nombres entiers ou des quotients de tels nombres. Ils avaient découvert qu’il était impossible d’exprimer de la sorte le rapport de la longueur de la diagonale d’un carré avec celle de son côté. Auraient-ils plus de chance avec le pentagone, la version étoilée étant leur signe de ralliement ?
Cet intérêt pour les polygones réguliers (côtés égaux) conduisit au problème de leur inscription dans un cercle en utilisant seulement la règle et le compas. Si la construction est facile pour le triangle, le carré ou l’hexagone, elle s’avère plus difficile pour le pentagone ou le décagone. Sa solution requiert la possibilité, dans les mêmes conditions, de découper un segment de droite en deux morceaux inégaux de sorte que la longueur du segment divisée par celle du grand morceau soit égale à la longueur du grand morceau divisée par celle du petit morceau. Cette valeur commune des deux rapports est le futur nombre d’or. Ce qui a frappé les Anciens, c'est la qualité particulière de ce rectangle qui manifeste … la "divine proportion", c'est-à-dire la représentation esthétique la plus harmonieuse d'une figure rectangulaire et nommée pour cela le "rectangle d'or".
. Euclide l’appelle la « division en moyenne et extrême raison » ou la « section ». Il montre comment résoudre le problème et applique le résultat pour inscrire dans une sphère deux des cinq polyèdres réguliers platoniciens : le dodécaèdre (douze faces pentagonales égales) et l’icosaèdre (vingt faces triangulaires égales). (Les « solides platoniciens » sont des polyèdres réguliers et convexes ; il existe seulement cinq solides de Platon. Par contre, les polygones réguliers et convexes de la géométrie plane sont en nombre infini.)
. À la renaissance italienne (début du XVIe siècle), le moine franciscain voyageur, exalté et mathématicien Fra Luca Pacioli réunit, dans un style enthousiaste, tout ce qu’Euclide et les pythagoriciens ont imaginé et découvert ou calculé, en un livre intitulé Divina proportione (1509). Les propriétés géométriques y sont étudiées, ainsi que ses relations avec certains polyèdres, dont le dodécaèdre qui représente l’univers chez Platon. Léonard de Vinci illustrera l’ouvrage avec 60 dessins de polyèdres (quelque 20 ans après avoir dessiné son Homme de Vitruve, aux proportions idéales inscrites symboliquement dans un cercle et un carré). Mais Luca Pacioli semble être le premier à y avoir ajouté une référence à l’esthétique de cette proportion. Le style particulier et ronflant de l’écrit remet le concept du nombre d’or au goût du jour. Son auteur, en proposant même un lien avec Dieu et la Sainte Trinité, fait avec sa « théologie géométrique » un pas vers une interprétation ésotérique.
L’astronome Kepler (1571-1630), lui, parlait de « joyau de la géométrie ».

Polyèdre régulier, illustration du traité de géométrie De Divina proportione.
. Ce n’est qu’aux XVIIe et XVIIIe siècles que des mathématiciens, avec le développement de la notation décimale et de l’algèbre, vont donner la valeur numérique du rapport de la division en moyenne et extrême raison : 1,618 034 … = (1+√5) / 2.
. . Au XIXe siècle, l’Allemagne voit l’essor d’une esthétique scientifique qui cherche à caractériser la beauté par un minimum de nombres. Sous l’impulsion d’Adolph Zeising (1810-1876), la section d’or, nouvel intitulé de la divine proportion, devient la norme esthétique. Le philosophe allemand produit un manifeste assez radical qui prétend que la section d’or est omniprésente – dans le corps humain, la structure des animaux, l’architecture, la peinture, la sculpture – et que sa présence rend les choses plus belles. En quelque sorte, il encapsule la beauté dans un seul nombre. Ses affirmations et ses mesures (notamment celles de la pyramide de Khéops et du Parthénon, en ruine) sont toutefois considérées comme approximatives et sujettes à caution.
. Mais c’est Matila Ghyka, prince et diplomate roumain, qui va véritablement lancer le mythe avec son ouvrage Le nombre d’or (écrit en français). C’est à lui que l’on doit une revisite détaillée de l’art et de l’architecture, et la « découverte » du nombre d’or dans les cathédrales, les temples grecs ou les tableaux de grands peintres.
La suite de Fibonacci
. La suite de Fibonacci commence ainsi :
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...
Ses deux premiers termes sont 0 et 1, et ensuite, chaque terme successif est la somme des deux termes précédents. Ainsi 0+1 = 1, 1+1 = 2, 1+2 = 3, 2+3 = 5, 3+5 = 8, etc. C’est la suite la plus simple.
Mais les deux nombres de départ pouvant être quelconques, il y a une infinité de suites possibles.
Son inventeur est Léonard de Pise (1175−v.1250), aussi connu sous le nom de Leonardo Fibonacci. Auteur de nombreux manuscrits mathématiques, il a entre autre rapporté d’Orient et démocratisé la notation numérique indo-arabe qui a remplacé pour les calculs la notation romaine peu pratique aux opérations arithmétiques, et a écrit et traduit des livres influents de mathématiques.
. Introduite comme problème récréatif dans son fameux ouvrage Liber Abaci, la suite de Fibonacci peut être considérée comme le tout premier modèle mathématique en dynamique des populations ! En effet, elle y décrit la croissance d’une population de lapins sous des hypothèses très simplifiées, à savoir : chaque couple de lapins, dès son troisième mois d’existence, engendre chaque mois un nouveau couple de lapins, et ce indéfiniment.
Partons donc d’un couple de lapins le premier mois. Le deuxième mois, on n’a toujours que ce même couple, mais le troisième mois on a déjà 2 couples, puis 3 couples le quatrième mois, 5 couples le cinquième mois, etc. La croissance de cette population est bel et bien décrite par la suite de Fibonacci.

. Leonard de Pise, dit Fibonacci (XIIe siècle), a introduit le nombre d’or dans ses célèbres séries, car pour toutes ces suites, le rapport entre deux termes consécutifs tend vers le nombre d'or φ (phi = 1,618 034 ...) :

Dans le Triangle de Pascal (ci-dessous) «, la somme des termes des diagonales de pente 1 forme la suite de Fibonacci :

Le nombre d’or, la clé de l’harmonie universelle
. Un rectangle d’or est un rectangle dit parfait en termes d’harmonie dont la longueur est φ fois plus grande que la largeur. Et si on dessine un carré sur une de ses longueurs, on obtient un rectangle plus grand qui lui aussi forme un rectangle d’or. En multipliant cette action on obtient la figure ci-dessous. Et si dans chacun des carrés obtenus, on dessine un quart de cercle, on obtient une spirale qui peut se prolonger dans l’infiniment grand comme dans l’infiniment petit. Celle-ci se nomme la spirale d’or.

Cette spirale, dite logarithmique, s'enfonce sans fin et tend rapidement vers un point O autour duquel elle s'enroule de plus en plus près. Ce point est appelé le centre de la spirale. Appelée spirale de Bernoulli, elle a de nombreuses propriétés. L'une d'elles est que la longueur du segment de droite est multipliée par le nombre d'or chaque fois que sa direction tourne d'un quart de tour, et croit donc suivant une progression géométrique.
. Quel est l'angle qui partage un cercle en section dorée ?
Faisons le ratio des aires des deux secteurs :
[ S (360 – x) / 360 ] / [ Sx / 360 ] et écrivons-le égal au nombre d’or ; on obtient :
360 = (1 + 1.618034) * x ; d’où :
x = 222.4924 °

Cet angle saillant, la divergence d’or, est égal à : 2Π / φ rd = 3.883 222 08 radians, soit 222° 29′ 32.0494″ (~ 222.5 °)
L'angle rentrant, l’angle d'or, est égal à : 2Π / φ2 rd = 2,399 963 23 radians, soit 137° 30′ 27.9505″ ( ~ 137.5°)
Remarquer que le ratio est indépendant de la surface, donc du diamètre du cercle, et il est aussi valable pour le périmètre.
. Le nombre d’or intervient également dans le pentagone régulier. Les cinq diagonales sont toujours φ fois plus grandes que les côtés du pentagone.

En découpant ce polygone en trois triangles, on obtient en son centre un triangle isocèle dont les deux cotés sont φ fois plus grands que la base : c’est le triangle d’or. Les deux autres triangles ont à l’opposé une base φ fois plus grande que les deux côtés. Eux sont appelés les triangles d’argent.
Avec des triangles d’or et des triangles d’argent, il est possible de remplir entièrement un plan infini. Ces pavages (dit de Penrose) sont remarquables parce qu’ils sont apériodiques. C’est à dire qu’ils ne possèdent aucune structure ou forme qui va se répéter (contrairement à un pavage fait de carrés ou d’hexagones) sans limite de taille du plan.

Le nombre d’or dans l’architecture
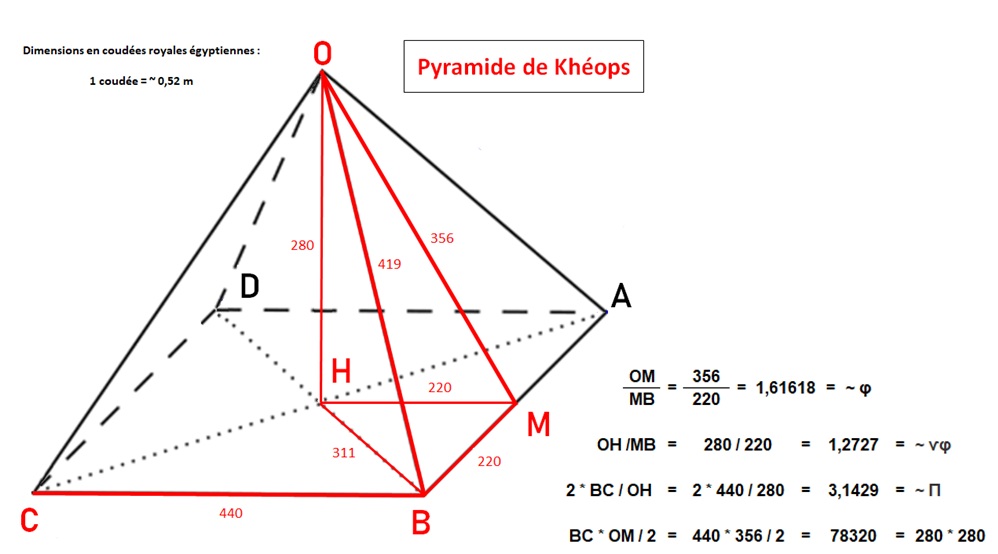
. Le nombre d’or, mystérieux et revêtant la forme symbolique, sera présent dans les Arts et d’abord dans l’architecture. On pense que sa découverte vient des pyramides de Khéops, mais cela n’est pas encore prouvé car on manque de preuves écrites.
En se livrant à des calculs, on peut trouver des ratios intéressants (amusants !) qui lieraient la pyramide de Khéops au nombre d’or :
. Les dimensions du Parthénon d’Athènes feraient apparaître le nombre d’or, dans son rapport longueur sur hauteur, selon les proportions du rectangle d’or. La présence de la divine proportion dans le Parthénon a été bien souvent controversée. Toutefois certains éléments sembleraient bien s’inscrire dans une logique visant à utiliser le nombre d’or.

. Les gradins du théâtre d’Épidaure, réputé pour ses qualités acoustiques, construit en Grèce à la fin du IVe siècle av.JC, seraient répartis selon le nombre d’or. Il y a en effet 55 gradins construits en deux séries de 34 et 21 rangs ; or ce sont trois nombres successifs de la suite de Fibonacci et les rapports 34/21 et (34+21) / 34 sont très proches du nombre d’or. Les gradins semblent donc partagés en « extrême et moyenne raison »

. Au Moyen-âge, des cathédrales gothiques comme celles d’Amiens et d’Auxerre attestent de la présence du pentagone et du décagone. Il semble que ces figures fascinent les compagnons tailleurs de pierre et maçons qui souhaitent ainsi montrer leur savoir et savoir-faire tout en gardant secret les procédés de fabrication de leurs œuvres. Les bâtisseurs de cathédrales utilisaient une « règle » spéciale, dite des « maîtres de l’œuvre ». Elle comportait cinq parties d’inégales longueurs : la paume, la palme, l’empan, le pied et la coudée. Ces longueurs faisaient référence au corps humain et étaient standardisées, au moins pour les « initiés ». On peut passer d’une unité à l’autre en multipliant par le nombre d’or. Ainsi une paume plus une palme vaut un empan, une palme plus un empan vaut un pied, un empan plus un pied, une coudée.
Des grandes cathédrales européennes jusqu’au Taj Mahâl, immense monument funéraire élevé en Inde, le nombre d’or ordonnerait les proportions de nombreuses constructions.
. Certains artistes utiliseront, intentionnellement, par la suite le nombre d’or de façon affirmée et assumée. L’architecte Le Corbusier a ainsi défini un système de mesures proportionnelles qu’il a appelé le Modulor (concept architectural avec les rapports en lien avec le nombre d’or). Il en est ainsi de la Cité radieuse de Marseille, où Le Corbusier a explicitement utilisé le nombre d’or et la suite de Fibonacci.
Le nombre d’or dans la peinture
. La peinture est un des domaines d’étude les plus vastes du nombre d’or. Puisque celui-ci confère à la peinture un effet esthétique particulier, il est alors normal qu’on le retrouve fréquemment dans cette discipline. Des centaines d’artistes l’ont utilisé, mais ce qui paraît fort étrange c’est que dans la majorité des cas, ces artistes ne l’ont probablement pas fait exprès.
Le premier utilisateur du nombre d’or dans le domaine de la peinture fut Jicopo de Barbari, qui représenta le célèbre mathématicien italien Fra Luca Pacioli (il a écrit en 1498 son fameux traité sur le nombre d’or : De Divina Proportione) expliquant un théorème à son élève : le pouce et l’index de la main gauche du mathématicien partageraient la hauteur du livre selon les proportions du nombre d’or.

Dans ce portrait de Luca Pacioli, auteur de De divina proportione, un dodécaèdre régulier est exposé en bas à droite. Jacopo de’ Barbari
. Dans le tableau « La Naissance De Venus », peint par Botticelli vers 1485 après la commande de Giovanni di Pier Francesco de Médicis, Botticelli représente la déesse du Temps recouvrant d’un manteau Vénus, déesse romaine de l’amour et de la beauté, née de l’écume de la mer d’après la mythologie : le monde idéal avec la naissance de l’humanité.
Botticelli y met en évidence la divine proportion de nombreuses façons dans ce tableau :

Les dimensions du tableau 172,5 × 278,5 cm respectent précisément la proportion du nombre d’or. D’autre part, le groupe du vent (à gauche) et la déesse du Temps (à droite) occupent les rectangles d’or, et sont positionnés sur leur diagonale. Il est également possible de tracer deux cercles dont les diamètres correspondent aux côtés de ces rectangles d’or. Le cercle de gauche renferme le groupe des Vents et Vénus, le cercle de droite Vénus et le personnage de la Grâce.
. D’autres peintres auraient aussi cédé aux charmes du nombre d’or, sans que l’on sache véritablement si leurs utilisations étaient volontaires, fortuites, inconscientes ou intentionnelles, ou encore s’il s’agit simplement de fractions proches de Phi. C’est le cas notamment de Léonard de Vinci !

Les proportions du corps humain en harmonie seraient régies par le nombre d’or puisqu’on retrouverait le rapport 1,618 en calculant la :
- hauteur totale / hauteur du nombril
- distance du nombril au genou
- distance du genou à la plante des pieds
- distance entre les extrémités des doigts et le coude
- distance entre le poignet et le coude
- distance entre la ligne de l’épaule et le sommet de la tête
- 1ere phalange / la 2eme
- 2eme phalange / la 3eme…

Dans le célèbre croquis « L’homme de Vitruve », celui-ci est inscrit à la fois dans un cercle et un carré ; ces deux figures géométriques, symboliquement opposées mais emboitées, sont l’expression de l’union des contraires, de la dualité. Le rapport entre le côté du carré et le rayon du cercle est égal au nombre d’or, ainsi emblématique des proportions du corps humain. Léonard de Vinci, cependant, ne mentionne pas cette proportion lorsqu’il traite de la composition du corps humain.
. Si la reconstruction a posteriori d’une conception à base du nombre d’or semble bien arbitraire (et pas très difficile), il existe des cas, en peinture, où le nombre d’or est intentionnellement présent. Les peintres Monet, Degas, Cézanne l’ont également utilisé, et Dali et Picasso, bien sûr, … par jeu.
Le nombre d’or dans les autres arts
. La symbolique du nombre d’or, au-delà de la géométrie architecturale et picturale, se retrouve dans tous les Arts et en particulier la musique, chez le compositeur Iannis Xenakis ou encore la littérature dans le Cantique des colonnes (1922) de Paul Valéry.
Le nombre d’or dans la nature
. On rencontre fréquemment la spirale logarithmique dans la nature. Une spirale logarithmique, dite de Bernoulli, s'enfonce sans fin et tend rapidement vers un point O origine, autour duquel elle s'enroule de plus en plus près. Ce point est appelé le centre de la spirale.
On retrouve ainsi le nombre d‘or un peu partout dans la nature : les fleurs, l’ananas, la coquille de l’escargot, l’étoile de mer, les ailes du papillon, la forme des pépins dans une pomme, la toile de l’araignée, l’écartement entre les feuilles d’un arbre, dans l’ouragan ou la galaxie ...

. Sur cette branche de sapin certaines aiguilles sont tombées mais en laissant une trace sur la tige. Ces aiguilles ont poussé en obéissant à une loi naturelle de répartition qui se retrouve sur toutes les branches de sapin. Cela prouve d'une façon irréfutable l'existence du nombre d'or dans la nature. Il est étonnant que certains l'imaginent partout mais il est tout aussi étonnant que d'autres le combattent avec acharnement ou l'ignorent volontairement.

. Le nombre d’or est toujours assimilé à la beauté naturelle des plantes. C’est Léonard de Vinci qui a étudié la règle de répartition des éléments consécutifs des végétaux. Il nota que les feuilles se placent le long de la tige d’une manière particulière, avec un angle constant, plus connu sous le terme d’angle de « divergence ». Il remarqua, en particulier que les tournesols ont des arrangements spiralés, visibles à l’œil nu, au centre de la fleur.

AB = BC + CD et AB / BC = φ ; BC / CD = φ.

Queue de caméléon casqué (Chamaeleo calyptratus) formant la courbe en spirale rappelant la suite mathématique de Fibonacci.
. Dans le cœur de cette fleur, nous voyons que ce sont les graines qui dessinent la spirale logarithmique de Fibonacci, et le nombre des spirales dans le sens des aiguilles d'une montre et celui en sens inverse sont des termes successifs de la suite de Fibonacci. Cette progression se poursuit de manière constante durant toute la vie du tournesol selon l’angle d’or qui est égal à 137.5 degré.
. Cette constatation de De Vinci, a été étudiée par Vogel, chercheur à l’Université technique de München, qui, en 1979, a calculé que cet angle de divergence permet à la plante d’optimiser l’espace occupé et favoriserait l’exposition au soleil.
. Le nombre d’or se retrouve chez nombre d’autres végétaux. L’ordonnancement des écailles d'une pomme de pin ou de l'écorce d'un ananas induit des spirales ordonnées par des nombres entiers, souvent associés au nombre d’or. Sur la pomme de pin on observe 8 spirales, chacune formée de 13 écailles dans un sens et 13 spirales formées de 8 écailles dans l'autre sens. Les proportions de ces spirales ne sont pas très éloignées de celles d'une spirale d’or. C'est exactement pareil pour le nautile, tout ce qui ressemble à une spirale est attaché à la divine proportion.

. Les nombres 8 et 13 sont deux nombres consécutifs de la suite de Fibonacci et leur rapport est proche du nombre d'or. Un phénomène analogue se produit avec les étamines des tournesols, cette fois avec les couples d'entiers (21,34), (34,55) et (55, 89). Chacun de ces couples correspond à deux entiers consécutifs de la suite de Fibonacci.
. Marque divine ? Inscription du nombre d’or dans le code génétique ? Plusieurs interprétations de ce genre ont été proposées pour cette « phyllotaxie ». L’explication a été apportée par les physiciens contemporains Stéphane Douady et Yves Couder : il s’agit en réalité d’une conséquence de contraintes d’encombrement et d’optimisation de l’espace disponible qui conduit à la répartition liée au nombre d’or, et non pas un code génétique.
. Le bras humain est un exemple de suite arithmétique que l’on trouve partout dans la nature : 1 os du haut de bras est relié à 2 os de l’avant-bras, eux-mêmes reliés à 8 autres os du poignet qui à leur tour sont prolongés par 5 os de la main et 3 os dans chacun des doigts. 1, 2 ,3, 5, 8, on y retrouve la suite de Fibonacci. Le rapport de la longueur de l’avant-bras rapportée à celle de la main est égal au nombre d’or et cela vaut aussi pour les trois phalanges.

. On retrouve également ce rapport dans l’ADN avec le rapport entre la longueur et la largeur d’un cycle complet de la double hélice de la molécule d’ADN.

. La suite de Fibonacci et le nombre d’or sont des exemples d’objets fractals. La structure des nervures d’une feuille est identique à celle des branches d’un arbre. On a donc bien une même forme répétée à l’infini, à une échelle toujours plus petite, l’auto-similarité.

. La nature repose sur la géométrie fractale, car elle lui permet de créer des structures gigantesques avec une efficacité redoutable. C’est grâce à elle que le corps humain peut contenir 96.000 kilomètres de veines et artères, ou que 1,80 mètre de filament d’ADN peut être contenu dans le noyau d’une cellule. Si on mettait bout à bout la totalité de l’ADN d’un être humain, on atteindrait une longueur de 6,4 milliards de kilomètres.
Le nombre d’or a aussi une face plus sombre…
. Certaines références au nombre d’or relèvent de dérives regrettables, erreurs et propos douteux. Par exemple, un ingénieur tourné astrologue, Maurice Rougie, a publié en 1946 sous le pseudonyme de Dom Neroman, Le nombre d’or à la portée de tous. Cet ouvrage, non seulement propose des relations entre Phi et d’autres nombres célèbres aussi séduisantes que fausses, mais contient également des affirmations totalement dépourvues de sens arithmétique. Bien pire, en partant d’un canon de la beauté humaine imposant un rapport entre taille et hauteur du nombril égal à Phi, Dom Neroman n’a pas hésité à avancer certaines conclusions racistes.
. La beauté ne peut pas se réduire à un seul nombre : c’est réductionniste, triste et dangereux. Le nombre d’or est un concept intéressant qui a joué et joue encore un grand rôle dans divers domaines mathématiques, mais il faut rester vigilant face à certaines conséquences que certains en tirent, à sa prétendue universalité et aux considérations occultes dont il peut faire l’objet.
. En 1988, dans Le Pendule de Foucault, puis dans un ouvrage de 1990 intitulé Les Limites de l'Interprétation, l'écrivain Umberto Eco tourne en dérision l'interprétation à outrance des faits avérés ou légendaires de l'histoire. Il tire des dimensions d'un kiosque à journaux pris au hasard dans sa rue, le même genre d'informations et d'analyses que celles faites parfois sur la pyramide de Khéops. Il montre ainsi que lorsqu'on s'applique à essayer de trouver des nombres remarquables comme Pi, ou la distance de la Terre à la Lune, on peut les trouver facilement, même dans un objet du quotidien. Une recherche plus poussée dans les dimensions de la cabane permet de découvrir à peu près toutes les relations géométriques et les nombres que l’on veut : le rapport entre la hauteur et la largeur de la fenêtre arrière est miraculeusement 3,142 (presque le nombre Pi), l’épaisseur de la tablette donne, aux unités près bien entendu, le même nombre que celui de la distance de la Terre au Soleil, ...
. La date de la bataille de Poitiers et la formule chimique de la naphtaline ont également été retrouvées.
